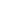LayerNorm与Softmax的online化与并行化

现代神经网络中有不少算子需要先做归约（reduction），再基于reduction的结果来对每个元素进行处理。这类算子会带来一些问题，如：

• 难以并行计算：原始的语义是序列化的，难以在GPU这样的并行计算硬件上加速。
• Overflow风险：如果是累加的话，当元素多或者元素大时，可能会超过浮点表示范围。

接下来以深度学习中常见的Softmax与LayerNorm算子为例看看这些问题在业界是如何被解决的。

Softmax

Softmax在深度神经网络中应用广泛，像计算logits，Transformer中的Attention，或是MoE中的门控中都有用到。先来看其数学定义：
$$y_i=\frac{e^{x_i}}{{\sum }_{j=1}^V{e}^{x_j}}$$
其中$x,y\in {\mathbb{R}}^V$。

按定义进行计算的Naive softmax是个2-pass算法。即先遍历所有元素做一次reduction操作求出分母（即normalization term），再遍历一遍元素计算每个$y_i$。

但由于计算机的浮点精度表示范围有限，现实当中，这种累加非常容易overflow。为了数值稳定性，通常会让每个数减去最大值。
$$y_i=\frac{e^{x_i-{\max }_{k=1}^V{x}_k}}{{\sum }_{j=1}^V{e}^{x_j-{\max }_{k=1}^V{x}_k}}$$
由于分子与分母中的$e^{-{\max }_{k=1}^V{x}_k}$一项可以被提出并被约掉，因此这样的改动不会影响最终结果。另外由于每个元素减去最大值，使得求和中的每一项不会超过1，这样和就不容易overflow。这种算法称为safe softmax。但是，代价是原算法成了3-pass算法，因为求最大值本身也是个reduction操作。

这三个pass，前两个pass是为了得到maximum value与normalization term。2018年来自Nvidia的论文《Online normalizer calculation for softmax》（也就是后来大名鼎鼎的Flash Attention的基石）将前两个pass合成一个。在合成的这个pass中，以online的方式计算：
m j = max ⁡ ( m j − 1 , x j ) d j = d j − 1 e m j − 1 − m j + e x j − m j

$$\begin{align*} m_j & = \max(m_{j-1}, x_j) \\ d_j & = d_{j-1} e^{m_{j-1} - m_j} + e^{x_j - m_j} \end{align*}$$ mj​dj​​=max(mj−1​,xj​)=dj−1​emj−1​−mj​+exj​−mj​​
第二次遍历后用下面公式计算所有值：
$$y_i=\frac{e^{x_i}-m_V}{d_V}$$
这样，在解决了overflow问题的基础上，还没增加pass数量。但这是一个序列化的计算过程，难以被GPU加速。为了能够被GPU加速，还需要将算法并行化。上面的算法可被写成：
$$\left[\begin{array}{c}{m}_V\\ d_V\end{array}\right]=\left[\begin{array}{c}{x}_1\\ 1\end{array}\right]\otimes \left[\begin{array}{c}{x}_2\\ 1\end{array}\right]\otimes \cdots \otimes \left[\begin{array}{c}{x}_V\\ 1\end{array}\right]$$
其中$\otimes$定义为：
$$\left[\begin{array}{c}{m}_i\\ d_i\end{array}\right]\otimes \left[\begin{array}{c}{m}_j\\ d_j\end{array}\right]=\left[\begin{array}{c}\max (m_i,m_j)\\ d_i\times e^{m_i-\max (m_i,m_j)}+d_j\times e^{m_j-\max (m_i,m_j)}\end{array}\right]$$
它满足结合律。这意味着我们可以把它切分成多块，分别交给不同的计算单元计算，然后将它们的结果进行下一轮进行计算，直到得到最终结果。这样就给Flash Attention中对GEMM+softmax+GEMM进行tiling打下了理论基础。

下面看代码。这是官方实现：https://github.com/NVIDIA/online-softmax。先看调用的地方：

online_softmax<256><<<batch_size,256>>>(x, y, V);
AI写代码cpp
1

输入为$bs\times V$的矩阵，需要对每一行进行softmax。Thread block个数为$bs$，每个thread block包含256个线程，负责处理一行 。

struct __align__(8) MD
{   
    float m;
    float d;
};      
        
__device__ __forceinline__ MD reduce_md_op(MD a, MD b)
{       
    bool a_bigger = (a.m > b.m);
    MD bigger_m = a_bigger ? a : b;
    MD smaller_m = a_bigger ? b : a;
    MD res;
    res.d = bigger_m.d + smaller_m.d * __expf(smaller_m.m - bigger_m.m);
    res.m = bigger_m.m;
    return res;
}       

template<int THREADBLOCK_SIZE>
__launch_bounds__(THREADBLOCK_SIZE)
__global__ void online_softmax(
    const float * __restrict x,
    float * __restrict y,
    int V)
{
    int thread_id = threadIdx.x;
    int vector_id = blockIdx.x;

    // reposition x and y to data for the current vector
    x += vector_id * V;
    y += vector_id * V;

    typedef cub::BlockReduce<MD, THREADBLOCK_SIZE> BlockReduce;

    __shared__ typename BlockReduce::TempStorage temp_storage;
    __shared__ MD md_total;

    MD md_partial;
    md_partial.m = -FLT_MAX;
    md_partial.d = 0.0F;
    for(int elem_id = thread_id; elem_id < V; elem_id += THREADBLOCK_SIZE)
    {
        MD new_elem;
        new_elem.m = x[elem_id];
        new_elem.d = 1.0F;
        md_partial = reduce_md_op(md_partial, new_elem);
    }

    MD md = BlockReduce(temp_storage).Reduce(md_partial, reduce_md_op);
    if (thread_id == 0)
        md_total = md;
    __syncthreads();

    float d_total_inverse = __fdividef(1.0F, md_total.d);
    for(int elem_id = thread_id; elem_id < V; elem_id += THREADBLOCK_SIZE)
        y[elem_id] = __expf(x[elem_id] - md_total.m) * d_total_inverse;
}
AI写代码cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

结构体MD包含m与d两个统计量，一个是maximum value，另一个是normalization term。reduce_md_op()函数为论文Algorithm 3的line 4,5。首先，每个线程把自己要做的先做完，然后用了cub这个库的BlockReduce进行跨block的reduce。最终的m与d放在shard memory中。这个过程如图：

最后每个线程基于它们分别处理对应的元素（论文Algorithm 3的line 8）。

LayerNorm

LayerNorm（LN）在论文中《Layer Normalization》中提出。相比在视觉类模型中广泛应用的BatchNorm（BN），它更适用于语言类模型。像Transformer中就有它的身影。RMSNorm是它的简化变体。

LayerNorm的的数学定义如下：
$$y=\frac{x-E[x]}{\sqrt{V[x]+ϵ}}\gamma +\beta$$
计算过程中需要对所有元素做reduction操作求均值与方差。对于给定的样本，均值与方差可以用下面公式计算：
μ n = 1 n ∑ i = 1 n x i σ n 2 = 1 n − 1 ∑ i = 1 n ( x i − μ n ) 2

$$\begin{align*} \mu_n & = \frac{1}{n} \sum_{i=1}^{n} x_i \\ \sigma^2_n & = \frac{1}{n - 1} \sum_{i=1}^n (x_i - \mu_n)^2 \end{align*}$$ μn​σn2​​=n1​i=1∑n​xi​=n−11​i=1∑n​(xi​−μn​)2​
显然，如果直接按定义来算，需要将数据过遍历两遍，分别计算均值与方差。这不只是影响效率，就像前面提到的，还有数值稳定性问题。这里累加元素是平方，容易导致overflow。

要将之改成1-pass算法倒还比较容易，可以用概率统计中常用的公式：
$$V(X)=E[(X-\mu {)}^2]=E(X^2)-E(X{)}^2$$
但这样仍然有数据稳定性问题。不仅容易overflow，而且还可能有catastrophic cancellation问题（两个接近的浮点数相减可能导致很大的相对误差）。

于是就引出了Welford算法。它由B. P. Welford在1962年的论文《Note on a method for calculating corrected sums of squares and products. Technometrics》中提出。另初始$M_1=x_1$，$S_1=0$，则有：
M k = M k − 1 + ( x k − M k − 1 ) / k S k = S k − 1 + ( x k − M k − 1 ) ( x k − M k )

$$\begin{align*} M_k & = M_{k-1} + (x_k - M_{k - 1}) / k \\ S_k & = S_{k-1} + (x_k - M_{k - 1}) (x_k - M_k) \end{align*}$$ Mk​Sk​​=Mk−1​+(xk​−Mk−1​)/k=Sk−1​+(xk​−Mk−1​)(xk​−Mk​)​
它维护在第k个样本到来时的均值估计$M_k$，用于更新二阶统计量$S_k$。基于它可以得到方差的估计。

这样，就把方差的计算online化了。它不仅是1-pass算法，而且数值稳定性还好。看起来很不错，要是能被GPU并行起来就更好了。于是，1979年Tony F. Chan等人的论文《Updating Formulae and a Pairwise Algorithm for Computing Sample Variances》提出了计算方差的并行算法。设样本数量为n，如果将之分为[1,m]和[m+1,n]两个部分，则有：
$$S_{1,m+n}=S_{1,m}+S_{m+1,m+n}+\frac{m}{n(m+1)}(\frac{m+n}{m}{T}_{1,m}-T_{1,n+m}{)}^2$$
其中$T_{1,m}={\sum }_{i=1}^m{x}_i$。这意味着我们可以将一段数据分成两段，交给不同的计算单元分别计算，然后放在一起修正更新。

接下来看下代码。这里主要参考apex中的实现：https://github.com/NVIDIA/apex/blob/master/csrc/layer_norm_cuda_kernel.cu。对于LayerNorm算子，在GPU上，cuda_layer_norm()函数会调用HostApplyLayerNorm()函数，继而调用CUDA kernel函数cuApplyLayerNorm()。

auto stream = at::cuda::getCurrentCUDAStream().stream();                          
const dim3 threads(32,4,1);                                                       
const uint64_t maxGridY = at::cuda::getCurrentDeviceProperties()->maxGridSize[1]; 
const dim3 blocks(1, std::min((uint64_t)n1, maxGridY), 1);                        
int nshared =                                                                     
    threads.y > 1 ?                                                               
        threads.y*sizeof(U)+(threads.y/2)*sizeof(U) :                             
        0;                                                                        
cuApplyLayerNorm<<<blocks, threads, nshared, stream>>>(                           
  output, mean, invvar, input, n1, n2, U(epsilon), gamma, beta);                  
AI写代码cpp
1
2
3
4
5
6
7
8
9
10

输入是一个n1 x n2的矩阵，n2是要normalization的维度。启动kernel时有n1个thread block，每个thread block有4个warp，即一个thread block中有128个threads。如图：

理想情况下thread block个数等于n1，即每个block处理一行数据。Block中的线程分摊行中元素。但如果n1太大超过限制，那一个thread block就需要处理多行，这也是外循环的作用。

for (auto i1=blockIdx.y; i1 < n1; i1 += gridDim.y) {
    cuWelfordMuSigma2(vals,n1,n2,i1,mu,sigma2,buf,rms_only); 
    const T* lvals = vals + i1*n2;   
    V* ovals = output_vals + i1*n2;  
    ...
}
AI写代码cpp
1
2
3
4
5
6

变量lvals与ovals分别是输入与输出起始位置指针。在每次迭代中，先调用cuWelfordMuSigma2()函数计算均值与方差。基于计算得到的均值与方差，根据LN或RMSNorm的公式得到结果。

接下来重点看下cuWelfordMuSigma2函数。该函数首先会有两个循环：

for (;  l+3 < n2;  l+=4*numx) {                    
  for (int k = 0;  k < 4;  ++k) {                  
    U curr = static_cast<U>(lvals[l+k]);           
    if (!rms_only) {                               
      cuWelfordOnlineSum<U>(curr,mu,sigma2,count); 
    } else {                                       
      cuRMSOnlineSum<U>(curr, sigma2);             
    }                                              
  }                                                
}                                                  
for (;  l < n2;  ++l) {                            
  U curr = static_cast<U>(lvals[l]);               
  if (!rms_only) {                                 
    cuWelfordOnlineSum<U>(curr,mu,sigma2,count);   
  } else {                                         
   cuRMSOnlineSum<U>(curr, sigma2);                
  }                                                
}                                                  
AI写代码cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

前一个循环每个线程处理4个元素。后一个循环在元素个数无法被4整除情况下处理剩余的数据。有点类似于loop unrolling或者vectorization中处理无法被整除的部分。这里的cuWelfordOnlineSum()函数用于LN的计算，cuRMSOnlineSum()用于RMSNorm。它们是序列化的，即每次考虑下一个元素。

每个线程将自己需要的都计算完后，就可以考虑线程间了。这里分两个阶段，首先是warp内的。由于warp内可以使用warp level primitive，无需shared memory。这里采用树型归约。warp包含32个线程，因此循环${\log }_{2}32=5$次。两两之间调用cuChanOnlineSum()函数计算。

// intra-warp reductions                                   
for (int l = 0;  l <= 4;  ++l) {                           
  int srcLaneB = (threadIdx.x+(1<<l))&31;                  
  U sigma2B = WARP_SHFL(sigma2, srcLaneB);                 
  if (!rms_only) {                                         
    U muB = WARP_SHFL(mu, srcLaneB);                       
    U countB = WARP_SHFL(count, srcLaneB);                 
    cuChanOnlineSum<U>(muB,sigma2B,countB,mu,sigma2,count);
  } else {                                                 
    cuChanRMSOnlineSum<U>(sigma2B, sigma2);                
  }                                                        
}                                                          
AI写代码cpp
1
2
3
4
5
6
7
8
9
10
11
12

这里的cuChanOnlineSum()函数就是前面提到的并行算法版本。具体可参考论文中的P4上的公式 2.1b。这里的后三个参数与前三个参数分别对应[1,m]与[m+1,m+n]两段。delta为$\frac{1}{n}{T}_{m+1,m+n}-\frac{1}{m}{T}_{1,m}$。

template<typename U> __device__
void cuChanOnlineSum(
  const U muB,
  const U sigma2B,
  const U countB,
  U& mu,
  U& sigma2,
  U& count)
{
  U delta = muB - mu;
  U nA = count;
  U nB = countB;
  count = count + countB;
  U nX = count;
  if (nX > U(0)) {
    nA = nA / nX;
    nB = nB / nX;
    mu = nA*mu + nB*muB;
    sigma2 = sigma2 + sigma2B + delta * delta * nA * nB * nX;
  } else {
    mu = U(0);
    sigma2 = U(0);
  }
}
AI写代码cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

计算完warp内后，就可以考虑warp间的，即thread block内的计算。有一种情况，就是一个block就一个warp。那就方便了，只要在warp内广播均值与方差即可：

if (!rms_only) {                      
  mu = WARP_SHFL(mu, 0);              
}                                     
sigma2 = WARP_SHFL(sigma2/U(n2), 0);  
AI写代码cpp
1
2
3
4

否则需要走更通用但更慢些的path：

U* ubuf = (U*)buf;                                                           
U* ibuf = (U*)(ubuf + blockDim.y);                                           
for (int offset = blockDim.y/2;  offset > 0;  offset /= 2) {                 
  // upper half of warps write to shared                                     
  if (threadIdx.x == 0 && threadIdx.y >= offset && threadIdx.y < 2*offset) { 
    const int wrt_y = threadIdx.y - offset;                                  
    if (!rms_only) {                                                         
      ubuf[2*wrt_y] = mu;                                                    
      ibuf[wrt_y] = count;                                                   
    }                                                                        
    ubuf[2*wrt_y+1] = sigma2;                                                
  }                                                                          
  __syncthreads();                                                           
  // lower half merges                                                       
  if (threadIdx.x == 0 && threadIdx.y < offset) {                            
    U sigma2B = ubuf[2*threadIdx.y+1];                                       
    if (!rms_only) {                                                         
      U muB = ubuf[2*threadIdx.y];                                           
      U countB = ibuf[threadIdx.y];                                          
      cuChanOnlineSum<U>(muB,sigma2B,countB,mu,sigma2,count);                
    } else {                                                                 
      cuChanRMSOnlineSum<U>(sigma2B,sigma2);                                 
    }                                                                        
  }                                                                          
  __syncthreads();                                                           
}                                                                            
// threadIdx.x = 0 && threadIdx.y == 0 only thread that has correct values   
if (threadIdx.x == 0 && threadIdx.y == 0) {                                  
  if (!rms_only) {                                                           
    ubuf[0] = mu;                                                            
  }                                                                          
  ubuf[1] = sigma2;                                                          
}                                                                            
__syncthreads();                                                             
if (!rms_only) {                                                             
  mu = ubuf[0];                                                              
}                                                                            
sigma2 = ubuf[1]/U(n2);                                                      
// don't care about final value of count, we know count == n2                
AI写代码cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

warp间与warp内的处理是类似的，也是采用树型规约。由于thread block中有4个warp，因此循环2次。在warp间只能用shared memory交换数据。这里的shared memory的buffer结构为：

每一次迭代中，一半warp的首线程将本warp的均值方差放入shared memory的buffer中，然后另一半warp的首线程从buffer中取出后用cuChanOnlineSum()函数进行归约。最后thread block中的首线程将最终的均值与方差放到shared memory的buffer中的最前两个位置。